 Long Answer Type
Long Answer TypeGiven: XY is a line parallel to side BC of a triangle ABC. BE || AC and CF || AB meet XY at E and F respectively.
To Prove: ar(ΔABE) = ar(ΔACF).
Proof: ∵ XY || BC | given
and CF || BX | ∵ CF || AB (given)
∴ □BCFX is a || gm
A quadrilateral is a parallelogram if its opposite sides are parallel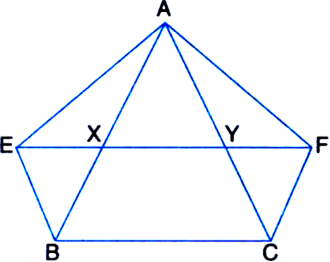
∴ BC = XF
| Opposite sides of a parallelogram are equal ⇒ BC = XY + YF ...(1)
Again,
∵ XY || BC | given
and BE || CY | ∵ BE || AC (given)
∴ □BCYE is a parallelogram
A quadrilateral is a parallelogram if its opposite sides are parallel
∴ BC = YE
| Opposite sides of a parallelogram are equal
⇒ BC = XY + XE ...(2)
From (1) and (2),
XY + YF = XY + XE
⇒ YF = XE
⇒ XE = YF ...(3)
∵ ΔAEX and ΔAYF have equal bases (∵ XE = YF) on the same line EF and have a common vertex A.
∴ Their altitudes are also the same.
∴ ar(ΔAEX) = ar(ΔAFY) ...(4)
∵ ΔBEX and ΔCFY have equal bases (∵ XE = YF) on the same line EF and are between the same parallels EF and BC (∵ XY || BC).
∴ ar(ΔBEX) = ar(ΔCFY) ...(5)
Two triangles on the same base (or equal bases) and between the same parallels are equal in area
Adding the corresponding sides of (4) and (5), we get
ar(ΔAEX) + ar(ΔBEX) = ar(ΔAFY) + ar(ΔCFY)
⇒ ar(ΔABE) = ar(⇒ACF).
 Short Answer Type
Short Answer TypeIn figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that
(i) ar(ΔACB) = ar(ΔACF)
(ii) ar(□AEDF) = ar(ABCDE). 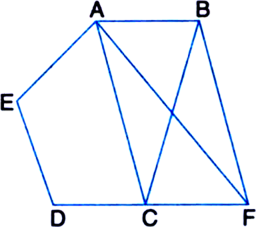
Show that the area of a rhombus is half the product of the lengths of its diagonals.
Or
Prove that the area of a rhombus is equal to half the rectangle contained by its diagonals.
