Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Areas of Parallelograms and Triangles

Long Answer Type

41. 8. XY is a line parallel to side BC of a triangle ABC. If BE || AC and CF || AB meet XY at E and F respectively, show that ar(ΔABE) = ar(ΔACF).

1117 Views

42. The side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed. Show that ar(||gm ABCD) = ar(||gm PBQR).

[Hint. Join AC and PQ. Now compare ar(ACQ) and ar(APQ)].

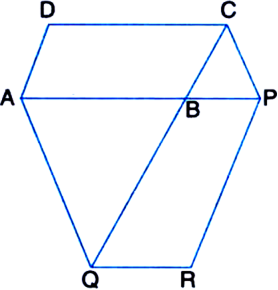
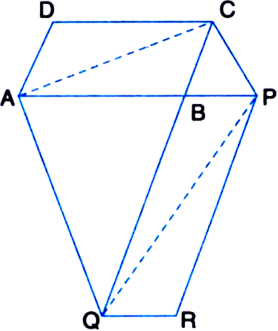
Given: The side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed.

To Prove: ar(|| gm ABCD) = ar(|| gm PBQR). Construction: Join AC and PQ.
Proof: ∵ AC is a diagonal of || gm ABCD

$therefore space ar left parenthesis increment ABC right parenthesis equals 1 half ar left parenthesis parallel to space gm space ABCD right parenthesis space space space space space space space space space space space space space space... left parenthesis 1 right parenthesis$
$because$ PQ is a diagonal of $parallel to$ gm BQRP
$therefore space space ar left parenthesis increment BPQ right parenthesis equals 1 half ar left parenthesis space parallel to space gm space BQRp right parenthesis space space space space space space space space space space space space space... left parenthesis 2 right parenthesis$

∵ ΔACQ and ΔAPQ are on the same base AQ and between the same parallels AQ and CP. ar(ΔACQ) = ar(ΔAPQ)
∵ Two triangles on the same base (or equal bases) and between the same parallels are equal in area
⇒ ar(ΔACQ) – ar(ΔABQ)
= ar(ΔAPQ) – ar(ΔABQ)
| Subtracting the same areas from both sides ⇒ ar(ΔABC) = ar(ΔBPQ)

$rightwards double arrow space 1 half ar left parenthesis space parallel to space gm space ABCD right parenthesis space equals space 1 half space ar left parenthesis space parallel to space gm space PBQR right parenthesis$

| From (1) and (2)
⇒ ar(|| gm ABCD) = ar(|| gm PBQR).

422 Views

Short Answer Type

43. Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O. Prove that ar(ΔAOD) = ar(ΔBOC).

286 Views

44.

In figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that
(i) ar(ΔACB) = ar(ΔACF)
(ii) ar(□AEDF) = ar(ABCDE).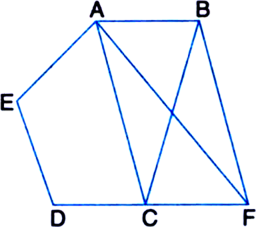

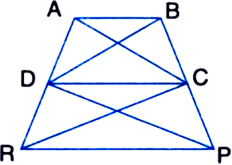
178 Views

45. A villager Itwaari has a plot of land of the shape of a quadrilateral. The Gram Panchayat of the village decided to take over some portion of his plot from one of the comers to construct a Health Centre. Itwaari agrees to the above proposal with the condition that he should be given equal amount of land in lieu of his land adjoining his plot so as to form a triangular plot. Explain how this proposal will be implemented.

201 Views

46. ABCD is a trapezium with AB || DC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar(ΔADX) = ar(ΔACY).

[Hint. Join CX.]

180 Views

47. In figure, AP || BQ || CR. Prove that ar(ΔAQC) = ar(ΔPBR).

114 Views

48. Diagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar(ΔAOD) = ar(ΔBOC). Prove that ABCD is a trapezium.

285 Views

49. Infigure, ar(ΔDRC) = ar(ΔDPC) and ar(ΔBDP) = ar(ΔARC). Show that both the quadrilateral ABCD and DCPR are trapeziums.

108 Views

50.

Show that the area of a rhombus is half the product of the lengths of its diagonals.

Prove that the area of a rhombus is equal to half the rectangle contained by its diagonals.

3361 Views