 Short Answer Type
Short Answer TypeGiven: Two points A and B and a positive real number k.
To find: The locus of a point P such that ar(ΔPAB) = k.
Construction: Draw PM ⊥ AB.
Determination: Let PM = h
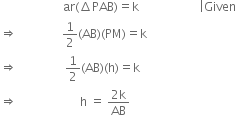
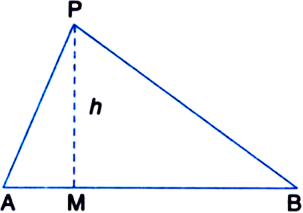
∵ Points A and B are given.
∴ AB is fixed.
Also, k being a positive real number k is fixed. ∴ h is a fixed positive real number.
∴ The locus of P is a line parallel to the line
AB at a fixed distance
![]()
on either side of it.
 Long Answer Type
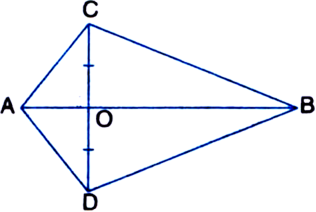
Long Answer TypeABCD is a parallelogram whose diagonals intersect at O. If P is any point on BO, prove that
(i) ar(ΔADO) = ar(ΔCDO)
(ii) ar(ΔABP) = ar(ΔCBP)
 Short Answer Type
Short Answer Type
 Long Answer Type
Long Answer Type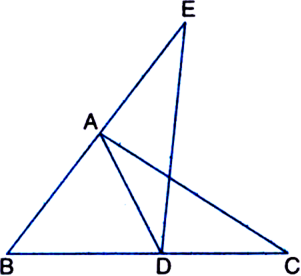
 Short Answer Type
Short Answer Type