 Short Answer Type
Short Answer Type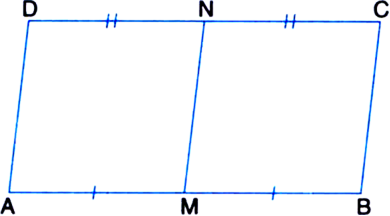
Similarly, we can prove that □MBCN is a parallelogram.
∵ || gm AMND and || gm MBCN are on equal bases AM and MB (∵ M is the mid-point of AB) and between the same parallels AB and DC.
∴ ar(|| gm AMND) = ar(|| gm MBCN).
 Long Answer Type
Long Answer TypeABCD is a parallelogram whose diagonals intersect at O. If P is any point on BO, prove that
(i) ar(ΔADO) = ar(ΔCDO)
(ii) ar(ΔABP) = ar(ΔCBP)
 Short Answer Type
Short Answer Type
 Long Answer Type
Long Answer Type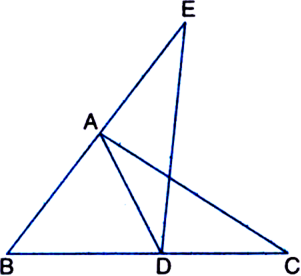
 Short Answer Type
Short Answer Type