Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Areas of Parallelograms and Triangles

Short Answer Type

51. Given two points A and B and a positive real number k. Find the locus of a point P such that ar(ΔPAB) = k.

149 Views

52. Show that the line segment joining the mid-points of a pair of opposite sides of a parallelogram divides it into two equal parallelograms.

385 Views

53. In an equilateral triangle, O is any point is the interior of the triangle and perpendiculars are drawn from O to the sides. Prove that the sum of these perpendicular line segments is constant.

552 Views

54. ΔABC and ΔABD are two triangles on the same base AB. If line segment CD is bisected by AB at O, show that ar (ΔABC) = ar (ΔABD).

312 Views

55. ΔABC and ΔABD are two triangles on the same base AB. If line segment CD is bisected by AB at O, show that ar (ΔABC) = ar (ΔABD).

ar left parenthesis quad. space ABCD right parenthesis equals 1 half BD. left parenthesis AM plus CN right parenthesis.

102 Views

Long Answer Type

56.
ABCD is a parallelogram whose diagonals intersect at O. If P is any point on BO, prove that

(i) ar(ΔADO) = ar(ΔCDO)
(ii) ar(ΔABP) = ar(ΔCBP)

Given: ABCD is a parallelogram whose diagonals intersect at O. P is any point on BO.

To Prove:

(i) ar(ΔADO) = ar(ΔCDO) (ii) ar(ΔABP) = ar(ΔCBP)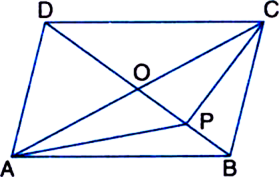

Given: ABCD is a parallelogram whose diagonals intersect at O. P is a

Proof:
(i)    ∵ Diagonals of a parallelogram bisect each other
∴ AO = OC
⇒ O is the mid-point of AC
DO is a median of ΔDAC
ar(ΔADO) = ar(ΔCDO)
∵ A median of a triangle divides it into two triangles of equal areas
(ii)    ∵ BO is a median of ΔBAC
∴ ar(ΔBOA) = ar(ΔBOC)    ...(1)
∵ A median of a triangle divides it into two triangles of equal areas ∵ PO is a median of ΔPAC
∴ ar(ΔPOA) = ar(ΔPOC)    ...(2)
∵ A median of a triangle divides it into two triangles of equal areas Subtracting (2) from (1), we get ar(ΔBOA) – ar(ΔPOA) = ar(ΔBOC) – ar(ΔPOC) ⇒    ar(ΔABP) = ar(ΔCBP)

158 Views

Short Answer Type

57. In the given figure, ΔABC is right angled at B, and BD is its median. E is the mid-point of BD. If AB = 6 cm, AC = 10 cm, calculate area of ΔBEC.

130 Views

Long Answer Type

58. In the given figure, ΔABC is right angled at A and AD is its median. BA is produced to E such that BA = AE. ED is joined. If AB = 6 cm, BC = 10 cm, find ar(ΔBED).

165 Views

59.

The medians of ΔABC intersect at G. Prove that

ar(ΔAGB) = ar(ΔAGC) = ar(ΔBGC) $equals 1 third space ar left parenthesis increment ABC right parenthesis$

293 Views

Short Answer Type

60. Triangles ABC and DBC are on the same base BC with vertices A and D on opposite sides of BC such that ar (ΔABC) = ar(ΔDBC). Show that BC bisects AD.

2446 Views