 Short Answer Type
Short Answer Type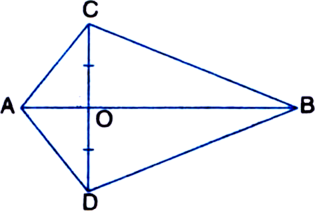
 Long Answer Type
Long Answer TypeABCD is a parallelogram whose diagonals intersect at O. If P is any point on BO, prove that
(i) ar(ΔADO) = ar(ΔCDO)
(ii) ar(ΔABP) = ar(ΔCBP)
 Short Answer Type
Short Answer Type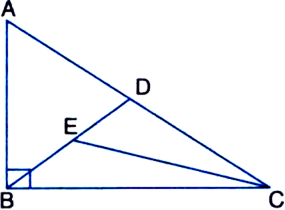
 Long Answer Type
Long Answer Type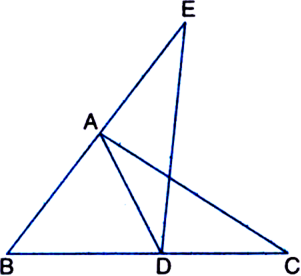
In right triangle BAC,
AB2 + AC2 = BC2
| By Pythagoras Theorem
⇒ 62 + AC2 = 102 ⇒ AC = 8 cm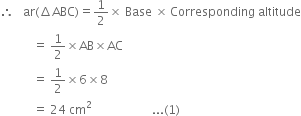
∵ AD is a median of ΔABC ∴ ar(ΔABD) = ar(ΔACD)
∵ A median of a triangle divides it into two triangles of equal areas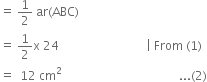
∵ BA = AE ∴ A is the mid-point of BE ∴ DA is a median of ΔBDE![]()
∵ A median of a triangle divides it into two triangles of equal areas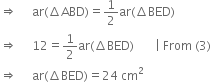
 Short Answer Type
Short Answer Type