 Short Answer Type
Short Answer Type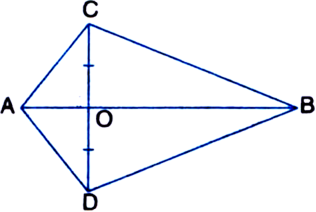
 Long Answer Type
Long Answer TypeABCD is a parallelogram whose diagonals intersect at O. If P is any point on BO, prove that
(i) ar(ΔADO) = ar(ΔCDO)
(ii) ar(ΔABP) = ar(ΔCBP)
 Short Answer Type
Short Answer Type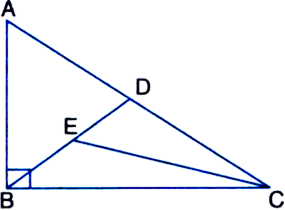
 Long Answer Type
Long Answer Type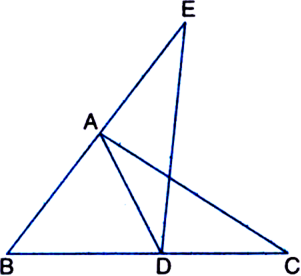
The medians of ΔABC intersect at G. Prove that
ar(ΔAGB) = ar(ΔAGC) = ar(ΔBGC) ![]()
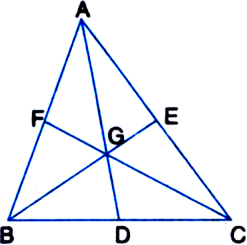
Given: The medians AD, BE and CF of ΔABC intersect at G.
To Prove: ar(ΔAGB) = ar(ΔAGC) ![]()
Proof: In ΔABC,
∵ AD is a median
∵ ar(ΔABD) = ar(ΔACD) ...(1)
A median of a triangle divides it into two triangles of equal areas
In ΔGBC,
∵ GD is a median ∴ ar(ΔGBD) = ar(ΔGCD) ...(2)
A median of a triangle divides it into two triangles of equal areas Subtracting (2) from (1), we get
ar(ΔABD) – ar(ΔGBD)
= ar(ΔACD) – ar(ΔGCD)
⇒ ar(ΔGAB) = ar(ΔGAC) ...(3)
Similarly, we can show that ar(ΔGAB) = ar(ΔGBC) ...(4)
From (3) and (4), we get ar(ΔGAB) = ar(ΔGAC) = ar(ΔGBC)
But,
ar(ΔGAB) + ar(ΔGAC) + ar(ΔGBC)
= ar(ΔABC)
⇒ 3 ar(ΔAGB) = ar(⇒ABC)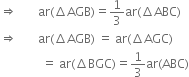
 Short Answer Type
Short Answer Type