 Short Answer Type
Short Answer Type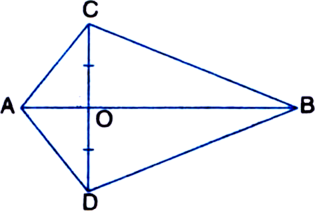
 Long Answer Type
Long Answer TypeABCD is a parallelogram whose diagonals intersect at O. If P is any point on BO, prove that
(i) ar(ΔADO) = ar(ΔCDO)
(ii) ar(ΔABP) = ar(ΔCBP)
 Short Answer Type
Short Answer Type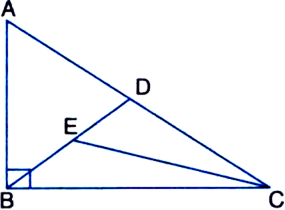
 Long Answer Type
Long Answer Type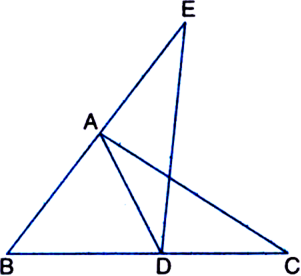
 Short Answer Type
Short Answer TypeGiven: Triangles ABC and DBC are on the same base BC with vertices A and D on opposite sides of BC such that ar(ΔABC) = ar(ΔDBC).
To Prove: BC bisects AD.
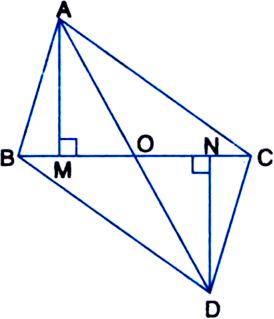
Proof: ar(ΔABC) = ar(ΔDBC) | Given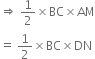
| Area of a triangle = ![]() x Base x Corresponding altitude
x Base x Corresponding altitude![]() AM = DN ...(1)
AM = DN ...(1)
In ΔAMO and ΔDNO,
AM = DN | From (1)
∠AMN = ∠DNO | Each = 90°
∠AOM = ∠DON
| Vertically opposite angles ∴ ΔAMO ⊥ ΔDNO
| AAS congruence rule ∴ AO = DO | CPCT
⇒ BC bisects AD.
