Short Answer Type
.
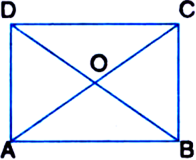
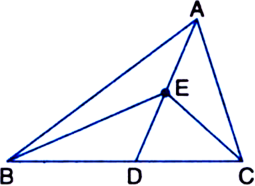
In figure, D and E are two points on BC such that BD = DE = EC. Show that ar(ΔABD) = ar(ΔADE) = ar(ΔAEC). [CBSE 2012 (March)]
Can you now answer the question that you have left in the ‘Introduction’, of this chapter, whether the field of Budhia has been actually divided into three parts of equal area?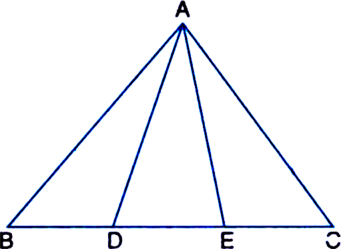
[Remark: Note that by taking BD = DE = EC, the triangle ABC is divided into three triangles ABD, ADE and AEC of equal areas. In the same way, by dividing BC into n equal parts and joining the points of division so obtained to the opposite vertex of BC, you can divide ΔABC into n triangles of equal areas.]
Long Answer Type
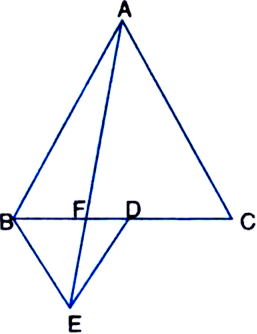
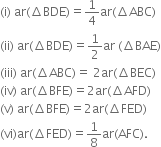
Given: ABC and BDE are two equilateral triangles such that D is the mid-point of BC. AE intersects BC at F.
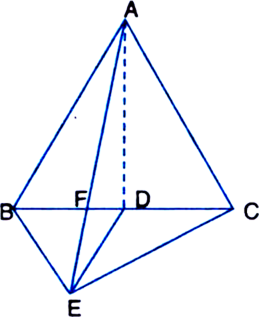
Proof: ∵ ΔABC is an equilateral triangle. ∴ ∠ABC = ∠BCA = ∠CAB = 60° ...(1)
∵ ΔBDE is an equilateral triangle.
∴ ∠BDE = ∠DEB = ∠EBD = 60° ...(2) ∠ABE + ∠BED
= ∠ABD + ∠EBD + ∠BED = 60°+ 60°+ 60°= 180°
∴ AB || DE ...(3)
∵ Sum of consecutive interior angles on
the same side of a transversal is 180° ∠EBA + ∠BAC
= ∠EBD + ∠DBA + ∠BAC = 60° + 60° + 60° = 180°
∴ AC || BE ...(4)
∵ Sum of consecutive interior angles on the same side of the transversal is 180°
∵ ΔCBA and ΔCEA are on the same base AC and between the same parallels.
∴ ar(ΔCBA) = ar(ΔCEA)
Two triangles on the same base (or equal bases) and between the same parallels are equal in area ⇒ ar(ΔABC) = ar(ΔCDA) + ar(ΔCED) + ar(ΔADE) ...(5)
In ΔABC,
∵ AD is a median.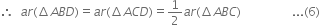
∵ A median of a triangle divides it into two triangles of equal area
In ΔEBC,
∵ ED is a median.
∵ A median of a triangle divides it into two triangles of equal area ∵ ΔDEA and ΔDBE are on the same base DE and between the same parallels AB and DE.
∴ ar(ΔDEA) = ar(ΔDBE) ...(8)
∵ Two triangles on the same base (or equal bases) and between the same parallels are equal in area
Using (6), (7) and (8), (5) gives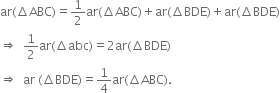
(ii) ∵ ΔBAE and ΔBCE are on the same base BE and between the same parallels BE and AC.
∴ ar(ΔBAE) = ar(ΔBCE)
∵ Two triangles on the same base (or equal bases) and between the same parallels are equal in
area
⇒ ar(ΔBAE) = 2 ar(ΔBDE)
| From (7)
(iii) 2 ar(ΔBEC) = 2.2 ar(ΔBDE)
| From (7)
= 4 ar(ΔBDE) = ar(ΔABC).
| Form (i)
(iv) ∵ ΔEBO and ΔEAD are on the same base ED and between the same parallels AB and DE.
∴ ar(ΔEBD) = ar(ΔEAD).
∵ Two triangles on the same base (or equal bases) and between the same parallels are equal in area ⇒ ar(ΔEBD) – ar(ΔEFD)
= ar(ΔEAD) – ar(ΔEFD)
| Subtracting the same areas from both sides ⇒ ar(ΔBFE) = ar(ΔAFD).
∵ Bases of ΔBDE and ΔABD are the same.
ar (ΔBEF) = ar(ΔAFD) ...(10) | From (iv)
Altuitude of 
Altitude of 
| From (9)
Altitude of 
Altitude of 
From (10) and (11),
BF = 2FD ...(12)
In ΔBFE and ΔFED,
∵ BF = 2FD and, alt (ΔBFE) = alt (ΔFED) ar(ΔBFE) = 2 ar(ΔFED).
(vi) Let the altitude of ΔABD be h.
Then, altitude of 
Now, 
From (13) and (14), we obtain,
Short Answer TypeDiagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that ar(ΔAPB) x ar(ΔCPD) = ar(ΔAPD) x ar(ΔBPC).
[Hint From A and C, draw perpendiculars to DD.]
Long Answer Type
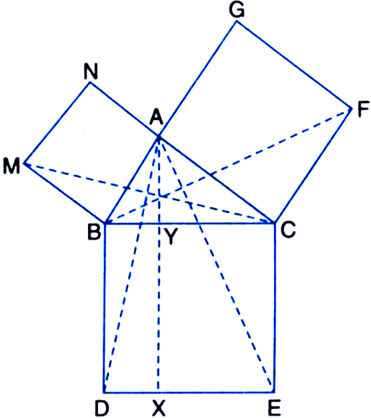
(i) ΔMBC ≅ ΔABD
(ii) ar(BYXD) = 2 ar(ΔMBC)
(iii) ar(BYXD) = ar(ΔABMN)
(iv) ΔFCB ≅ ΔACE
(v) ar(CYXE) = 2 ar(ΔFCB)
(vi) ar(CYXE) = ar(ACFG)
(vii) ar(BCED) = ar(ABMN) + ar(ACFG).
Note: Result (vii) is the famous Theorem of Pythagoras. You shall learn a simpler proof of this theorem in Class X.
Switch
