 Long Answer Type
Long Answer TypeIf the mth term of an A. P. is  and nth term is
and nth term is  then show that its (mn)th term is 1.
then show that its (mn)th term is 1.
Let x and d be the first term and common difference respectively of the AP, respectively.
Then,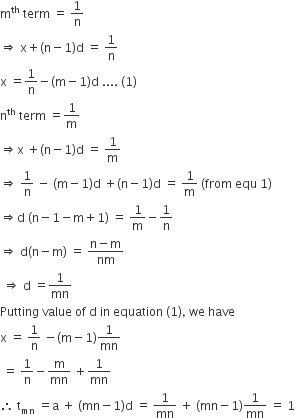
 Short Answer Type
Short Answer Type Long Answer Type
Long Answer TypeThe ratio of the sums of the first m and first n terms of an A. P. is m2: n2. Show that the ratio of its mth and nth terms is (2m−1):(2n−1).
 Short Answer Type
Short Answer TypeIn an AP, if the common difference (d) = –4, and the seventh term (a7) is 4, then find the first term.
 Long Answer Type
Long Answer TypeThe sum of four consecutive numbers in an AP is 32 and the ratio of the product of the first and the last term to the product of two middle terms is 7 : 15. Find the numbers.
 Multiple Choice Questions
Multiple Choice Questions Short Answer Type
Short Answer Type Long Answer Type
Long Answer TypeFind the number of terms of the AP -12, -9, -6,... 12. If 1 is added toeach term of this AP, then find the sum of all terms of the AP thusobtained.
