Short Answer TypeIn the figure below, ABC is a triangle in which ∠BAC = 30°. Show that BC is equal to radius of the circumcircle where centre is O.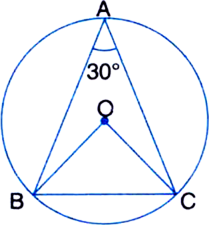
Long Answer TypeTwo chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
The lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance 4 cm from the centre, what is the distance of the other chord from the centre?
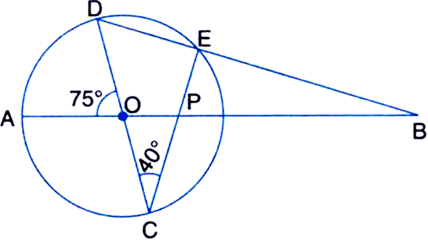
Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
Short Answer TypeLong Answer TypeAC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD are diameters, (ii) ABCD is a rectangle.
