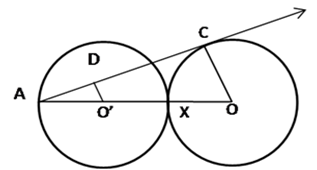
In given Fig. , two equal circles, with centres O and O’, touch each other at X. OO’ produced meets the circle with centre O’ at A. AC is tangent to the circle with centre O, at the point C. O’D is perpendicular to AC. Find the value of 

In the given figure, PQ is a chord of a circle with centre O and PT is tangent. If ∠QPT = 60^o, find ∠ PRQ.

In the given figure, two tangents RQ and RP are drawn from an external point R to the circle with centre O. If ∠PRQ = 120^o, then prove that OR = PR + RQ.

Prove that tangents drawn at the ends of a diameter of a circle are parallel to each other.

In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA = 12 cm, QC = QD = 3 cm, then find PC + PD.

Two tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that ∠PTQ = 2 ∠OPQ.

Prove that the lengths of tangents drawn from an external point to a circle are equal. 

A chord PQ of a circle of radius 10 cm subtends an angle of 60° at the centre of the circle. Find the area of major and minor segments of the circle. 

Prove that the lengths of tangents drawn from an external point to a circle are equal.

If the difference between the circumference and the radius of a circle is 37cm, then using $\mathrm{\pi } = \frac{22}{7}$ , the circumference (in cm) of the circle is:

• 154

• 44

• 14

• 7