Fill In the Blanks
Short Answer TypeA tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is :
(a) 12 cm (b) 13 cm
(c) 8.5 cm (d) 
From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is
(A) 7 cm (B) 12 cm
(C) 15 cm (D) 24.5 cm.
In Fig. 10.11, if TP and TQ are the two tangents to a circle with centre O so that ∠ POQ = 110°, then ∠ PTQ is equal to
(A) 60° (B) 70°
(C) 80° (D) 90°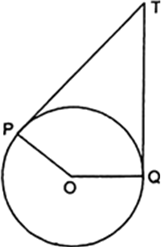
Fig. 10.11
Long Answer TypeIf tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80°, then ∠ POA is equal to
(A) 50° (B) 60°
(C) 70° (D) 80°.
In ΔPOA and ΔPOB
PA = PB
(Tangents from external point P)
OA = OB (Radii of a circle)
and OP = OP (common)
∴ ΔPOA ≅ ΔPOB
(by SSS congruency)
⇒ ∠OPA = ∠OPB
⇒ ∠OPA = ∠OPB = 40°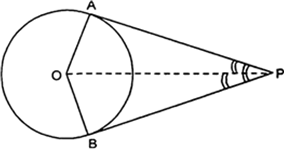
Since, the tangent at any point of a circle is perpendicular to the radius through the point of contact.
∴ ∠OAP = 90°
Now, in ΔOAP,
∠OAP + ∠OPA + ∠POA = 180°
⇒ 90° + 40° + ∠POA = 180°
⇒ 130 + ∠POA = 180°
⇒ ∠POA = 50°
So, right option is (A).
Short Answer TypeProve that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
Long Answer TypeTwo concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
Switch
