Short Answer Type
Short Answer Type
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.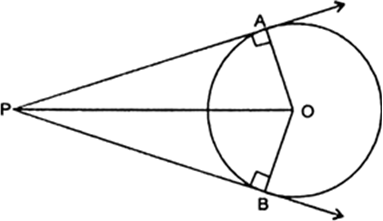
Given : PA and PB arc two tangents drawn from an external point P to a circle with centre O.
To prove : ∠AOB + ∠APB = 180°
Const : Join OA and OB.
Proof : ∵ The tangent at any point of circle is perpendicular to the radius through the point of contact.
∴ ∠OAP = 90° .....(i)
and ∠OBP = 90° .....(ii)
Adding (i) and (ii), we get
∠OAP + ∠OBP = 180°
Now in quadrilateral AOBP,
∠OAP + ∠OBP + ∠APB + ∠AOB = 360°
⇒ 180° + ∠APB + ∠AOB = 360°
∴ ∠APB + ∠AOB = 180°.
 Long Answer Type
Long Answer TypeA triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively (see Fig. 10.14). Find the sides AB and AC. 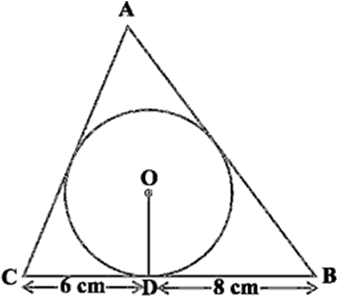
Fig, 10.14
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
 Short Answer Type
Short Answer Type