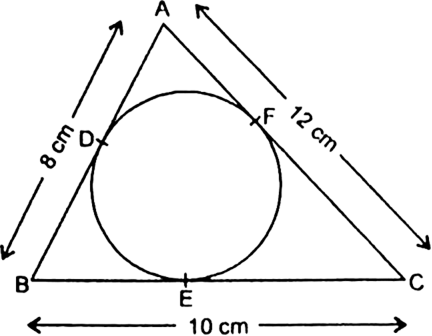
Short Answer Type
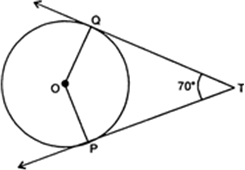
Since, the tangent at any point of a crcle is perpenedicular the radius throgh the point of contact.
∴ ∠OAT = 90°
and ∠OBT = 90°
If two tangents are drawn to a circle from an external point, then they are equally inclined to the segment joining the centre to the point
∴ ∠ATO = ∠BTO
But ∠ATO = 40°
Now, ∠BTO = 40°
In quadrilateral, ∠OBT, we have
∠OAT + ∠OBT + ∠ATB + ∠AOB= 360°
⇒ 90 + 90 + 80 + ∠AOB = 360°
⇒ 260 + ∠AOB = 360°
⇒ ∠AOB = 360° – 260° = 100°
Switch
