Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Circles

Short Answer Type

251. Two tangents TP and TQ are drawn from an external point T to a circle with centre O, as shown in figure. If they are inclined to each other at angle of 70°, then what is the value of ∠POQ?

115 Views

252. In the figure given below, PA and PB are tangents to the circle drawn from an external point P. CD is a third tangent touching the circle at Q. If PB = 10 cm and CQ = 2 cm, what is the length of PC?

2510 Views

253. The length of tangent from a point A at a distance of 5 cm from the centre of the circle is 4 cm. What will be the radius of the circle?

90 Views

254. What is the distance between two parallel tangents of a circle of the radius 4 cm?

1261 Views

255. Two tangents TP and TQ are drawn from an external point T to a circle with centre O, as shown in Fig. If they are inclined to each other at an angle of 100°, then what is the value of ∠POQ?

103 Views

256. In figure 2, if ∠ATO = 40°, find ∠AOB.

439 Views

257. Two tangents PA and PB are drawn to a cirlce with centre O from an external point P. Prove that ∠APB = 2∠OAB.

4819 Views

258. O is the centre of two concentric circles of radii 4 cm and 6 cm. PT and PS are tangents to the larger circle and smaller circle respectively from an external point P.PT = 10 cm, find the length of PS.

252 Views

259. A circle is inscribed in a ΔABC, having sides 8 cm, 10 cm, and 12 cm, as shown in Fig. Find AD, BE and CF.

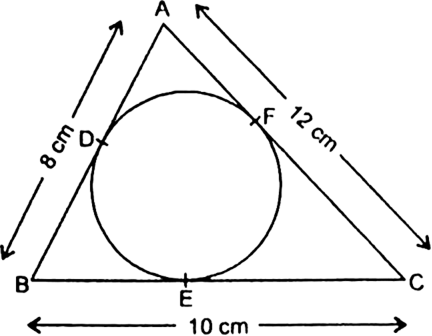
It is given that a circle inscribed in a ΔABC having sides.
AB = 8 cm,
BC = 10 cm
and    AC = 12 cm
Since, tangents drawn from an external points are equal.
So, AD = AF
BD = BE
and    CE = CF
Let AD = AF = x
BD = BE = y
and    CE = CF = z
AB = 8
⇒ AD + BD = 8
⇒ x + y = 8    ......(i)
∵ BC = 10
⇒    BE + CE = 10
⇒    y + z = 10    ....(ii)
∵ AC = 12
⇒ AF + CF = 12
⇒ x + z = 12    ...(iii)
Adding (i), (ii) and (iii), we get
2x + 2y + 2z = 30
⇒ 2(x + y + z) = 30
⇒    x + y + z = 15    ...(iv)
Putting the value of (i) in (iv), we get
8 + z = 15
⇒    z = 15 – 8
= 7 cm.
Putting the value of (ii) in (iv)
x + 10 = 15
⇒    x = 5 cm
Putting the value of (iii) in (iv), we get
y + 12 = 15 y = 3 cm
Hence,    x = AD = 5 cm
y = BE = 3 cm and    z = CF = 7 cm

117 Views

260. In figure, a circle touches all the four sides of a quadrilateral ABCD_/ whose sides AB = 6 cm, BC = 7 cm and CD = 4 cm. Find AD.

299 Views