Short Answer Type
Short Answer Type
 Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type
 Long Answer Type
Long Answer Type
It is given that ABC is a right angle triangle with AB = 6 cm and AC = 8 cm and a circle with centre O has been inscribed.
Using Pythagoras theorem, we get
BC2 = AC2 + AB2
= (8)2 + (6)2
= 64 + 36 = 100
⇒ BC = 10 cm
![]() Tangents at any point of a circle is perpendicular to the radius through the point of contact
Tangents at any point of a circle is perpendicular to the radius through the point of contact ![]()

= 3r + 4r + 5r
= 12r ...(ii)
Comparing (i) and (ii), we get
24 = 12r ⇒ r = 2 cm
Method – II:
In quadrilateral APOR,
∵ ∠OPA = ∠ORA = 90°
∠PAR = 90°
⇒ ∠OPA = ∠ORA = ∠PAR = ∠POR = 90° ....(i)
and AP = AR (ii) (length of tangents drawn from an external point are equal)
Using result (i) and (ii), we get
APOR is a square
Therefore,
OR = AR = r [Sides of square] and OR = AP = r [Sides of square]
Now, BP = AB – AP = 6 – r and, CR = AC – AR = 8 – r
Since tangents from an external point are equal
CR = CQ = 8 – r and BP = BQ = 6 – r
Now, In ΔABC,
BC2 = AC2 + AB2
⇒ (CQ + BQ)2 = (8)2 + (6)2
⇒ (8 – r + 6 – r)2 = 64 + 36
⇒ (14 – 2r)2 = 100
⇒ (14 – 2r)2 = (10)2
⇒ 14 – 2r = 10
⇒ –2r = –4
⇒ r = 2
Hence radius of circle (r) = 2 cm.
 Short Answer Type
Short Answer TypeFrom a point P outside a circle, with centre O tangents PA and PB are drawn as shown in the figure, prove that
(i) ⇒AOP = ∠BOP
(ii) OP is the perpendicular bisector of AB.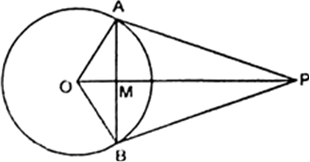
 Long Answer Type
Long Answer Type
 Short Answer Type
Short Answer Type