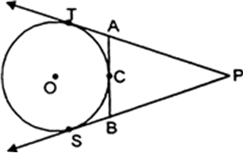
Short Answer Type
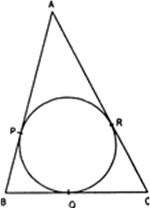
Short Answer TypeThe incircle of ΔABC touches the sides BC, CA and BA at D, E and F respectively. If
AB = AC, prove that BD = CD.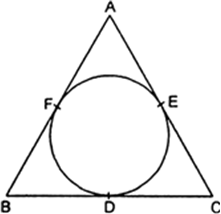
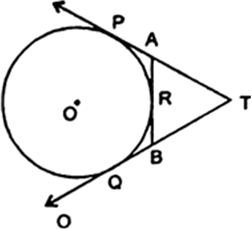
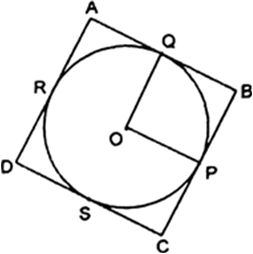
Length of tangents from same external point are equal
∴TP = TQ
AP = AR
and BR = BQ
We have, TP = TQ
⇒ TA + AP = TB + BQ
⇒ TA + AR = TB + BR
Hence Proved.
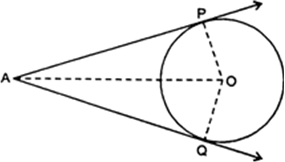
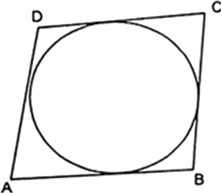
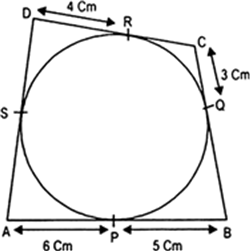
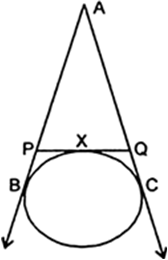
A quadrilateral ABCD is drawn to circumscribe a circle (Fig. 10.62). Prove that AB + CD = AD + BC.