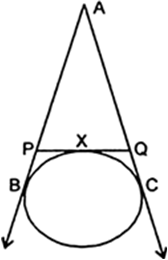
Short Answer Type
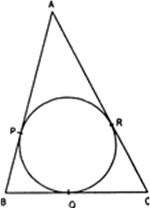
Short Answer TypeThe incircle of ΔABC touches the sides BC, CA and BA at D, E and F respectively. If
AB = AC, prove that BD = CD.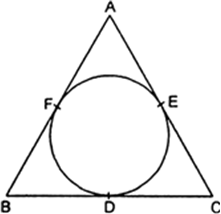
A quadrilateral ABCD is drawn to circumscribe a circle (Fig. 10.62). Prove that AB + CD = AD + BC.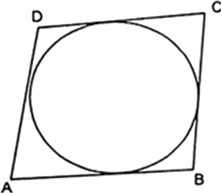
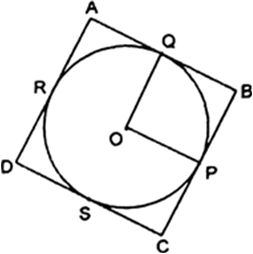
Let ABCD be a parallelogram and a circle with centre O. Let sides AB, BC, CD and AD of the parallelogram touch the circle at E, F, G and H respectively.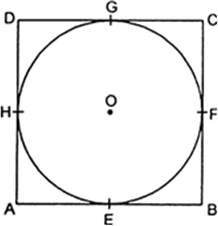
Since the length of two tangents drawn from an external point to a circle are equal.
So, AE = AH ...(i)
BE = BF ....(ii)
CG = CF ...(iii)
and DG = DH ....(iv)
Adding (i), (ii), (iii) and (iv), we get
AE + BE + GC + DG = AH + BF + CF + DH
⇒ (AE + BE) + (GC + DG)
= (AH + DH) + (BF + CF)
⇒ AB + CD = AD + BC