Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Circles

Short Answer Type

271.

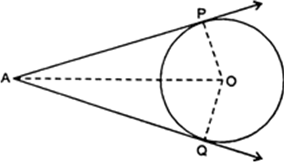
The incircle of ΔABC touches the sides BC, CA and BA at D, E and F respectively. If
AB = AC, prove that BD = CD.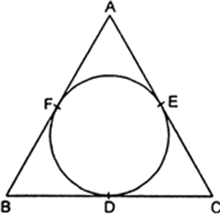

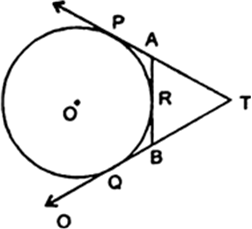
108 Views

272. In Figure 7, TP and TQ are tangents from T to the circle with centre O and R is any point on the circle. If AB is a tangent to the circle is R, prove that TA + AR = TB + BR.

721 Views

273. Prove that the lengths of tangent s drawn from an external point to a circle are equal.

90 Views

274.

A quadrilateral ABCD is drawn to circumscribe a circle (Fig. 10.62). Prove that AB + CD = AD + BC.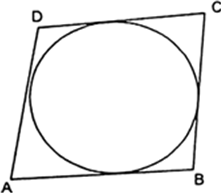

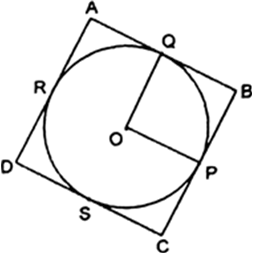
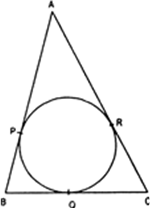
113 Views

275. In Figure, a circle is inscribed in a quadrilateral ABCD in which DB = 90°. If AD = 23 cm. and DS = 5 cm. find the radius (r) of the circle.

490 Views

276. ABC is a isosceles triangle in which AB = AC circumscribed about a circle. Show that BC is bisected at the point of contact.

227 Views

277. In Fig. 10.65A, quadrilateral ABCD is circumscribing a circle. Find the perimeter of the quadrilateral ABCD.

203 Views

278. A circle is inscribed in a ΔABC, touching AB, BC and AC at P,Q and R respectively, as shown in Fig. 10.65 B. If AB = 10 cm, AR = 7 cm and RC = 5 cm, then find the length of BC.

AP = AR
BP = BQ
CR = CQ
[Tangents from internal points are equal.]
Adding, we get
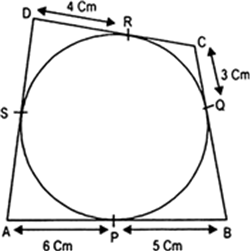
AP + BP + CQ = AR + BQ + CQ
⇒ (AP + BP) + CR = AR + (BQ + CQ)
⇒ AB + 5 = 7 + BC
⇒ 10 + 5 = 7 + BC
⇒ BC = 15 – 7 = 8 cm.

111 Views

279. Using the above, do the following : In Fig., from a point P, tangents PT and PS are drawn to a circle with centre O. At a point C on the circle, another tangent is drawn to the circle to intersect PT in A and PS in B. If PT = 12 cm and BC = 5 cm, find the length of PB.

84 Views

280. If AB, AC, PQ are tangents in figure, and AB = 7 cm, and XQ = 2 cm, find the length of AQ.

127 Views