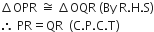Multiple Choice QuestionsChord
Short Answer TypeIn Fig. , PQ is tangent at point C to a circle with centre O. If AB is a diameter and ∠CAB = 30°, find ∠PCA.
In Fig.2, a quadrilateral ABCD is drawn to circumscribe a circle, with centre O, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, R and S respectively. Prove that AB + CD = BC + DA.
In Fig, from an external point P, two tangents PT and PS are drawn to a circle with centre O and radius r. If OP=2r, show that ∠ OTS = ∠ OST = 30°.
In Fig. , O is the centre of a circle such that diameter AB = 13 cm and AC = 12 cm. BC is joined. Find the area of the shaded region. (Take π = 3.14)
Prove that the lengths of the tangents drawn from an external point to a circle are equal.
Construction: Draw a circle centred at O.
Let PR and QR are tangent drawn from an external point R to the circle
Switch
