Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

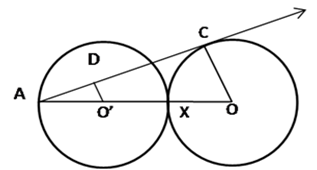
In given Fig. , two equal circles, with centres O and O’, touch each other at X. OO’ produced meets the circle with centre O’ at A. AC is tangent to the circle with centre O, at the point C. O’D is perpendicular to AC. Find the value of $DO to the power of apostrophe over CO$

3422 Views

322.
In the given figure, PQ is a chord of a circle with centre O and PT is tangent. If ∠QPT = 60^o, find ∠ PRQ.

PQ is the chord of the circle and PT is tangent.

We know that the tangent to a circle is perpendicular to the radius through the point of contact.

∴ ∠ OPT = 90^o

Now, Given

∠ QPT = 60^o

∴ ∠ OPQ = ∠OPT - ∠QPT

⇒ ∠ OPQ = 90^o - 60^o = 30^o

In Δ OPQ,

OP= OR (Radii of the same circle)

∠ OQP = ∠ OPQ = 30^o (in a triangle, equal sides have equal angles opposite to them.)

Now,

∠ OQP + ∠OPQ + ∠POQ = 180^o [Angle sum property]

⇒ 30^o + 30^o + ∠POQ = 180^o

⇒ ∠POQ = 180^o - 60^o = 120^o

⇒ Reflex ∠POQ = 360^o -120^o = 240^o

We know that the angle subtended by an arc of a circle at the centre is twice the angle subtended by it any point on the remaining part of the circle.

Therefore,

Reflex ∠POQ = 2 ∠PRQ

⇒ 240^o = 2 ∠PRQ

⇒ ∠PRQ = 240 / 2 = 120^o

Hence, the measure of angle PRQ is 120^o.

3511 Views

323.

In the given figure, two tangents RQ and RP are drawn from an external point R to the circle with centre O. If ∠PRQ = 120^o, then prove that OR = PR + RQ.

2137 Views

324.

Prove that tangents drawn at the ends of a diameter of a circle are parallel to each other.

3330 Views

325.

In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA = 12 cm, QC = QD = 3 cm, then find PC + PD.

8295 Views

326.

Two tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that ∠PTQ = 2 ∠OPQ.

3153 Views

Long Answer Type

327.

Prove that the lengths of tangents drawn from an external point to a circle are equal.

1719 Views

328.

A chord PQ of a circle of radius 10 cm subtends an angle of 60° at the centre of the circle. Find the area of major and minor segments of the circle.

5151 Views

Short Answer Type

329.

Prove that the lengths of tangents drawn from an external point to a circle are equal.

Multiple Choice Questions

330.

If the difference between the circumference and the radius of a circle is 37cm, then using $π = \frac{22}{7}$ , the circumference (in cm) of the circle is: