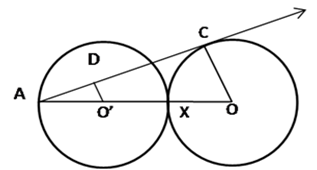
Short Answer TypeIn given Fig. , two equal circles, with centres O and O’, touch each other at X. OO’ produced meets the circle with centre O’ at A. AC is tangent to the circle with centre O, at the point C. O’D is perpendicular to AC. Find the value of 
In the given figure, PQ is a chord of a circle with centre O and PT is tangent. If ∠QPT = 60o, find ∠ PRQ.
In the given figure, two tangents RQ and RP are drawn from an external point R to the circle with centre O. If ∠PRQ = 120o, then prove that OR = PR + RQ.
Prove that tangents drawn at the ends of a diameter of a circle are parallel to each other.
Let AB be the diameter of a circle, with centre O. The tangents PQ and RS are drawn at points A and B, respectively.
We know that a tangent at any point of a circle is perpendicular to the radius through the point of contact.
∴ OA ⊥ PQ and OB ⊥ RS
⇒ ∠OBR = 90°
∠OBS = 90°
∠OAP = 90°
∠OAQ = 90°
We can observe the following:
∠OBR = ∠OAQ and ∠OBS = ∠OAP
Also, these are the pair of alternate interior angles.
Since alternate interior angles are equal, the lines PQ and RS are parallel to each other.
Hence, proved.
In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA = 12 cm, QC = QD = 3 cm, then find PC + PD.
Two tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that ∠PTQ = 2 ∠OPQ.
Long Answer TypeProve that the lengths of tangents drawn from an external point to a circle are equal.
A chord PQ of a circle of radius 10 cm subtends an angle of 60° at the centre of the circle. Find the area of major and minor segments of the circle.
Short Answer Type
Multiple Choice QuestionsIf the difference between the circumference and the radius of a circle is 37cm, then using , the circumference (in cm) of the circle is:
154
44
14
7
Switch
