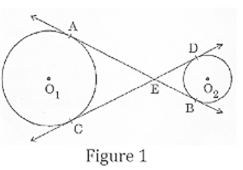
Short Answer TypeIn Figure 1, common tangents AB and CD to the two circles with centres O1 and O2 intersect at E. Prove that AB = CD.
The incircle of an isosceles triangle ABC, in which AB = AC, touches the sides BC, CA and AB at D, E and F respectively. Prove that BD = DC.
Long Answer TypeProve that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
Given: A circle C ( 0, r ) and a tangent l at point A.
To prove: OA l
Construction: Take a point B, other than A, on the tangent l. Join OB. Suppose OB meets the circle in C.
Proof: We know that, among all line segment joining the point O to a point on l, the perpendicular is shortest to l.
OA = OC (Radius of the same circle)
Now, OB = OC + BC.
But among all the line segments, joining the point O to a point on AB, the shortest one is the perpendicular from O on AB.
Hence OA is perpendicular to l.
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Short Answer TypeIf the angle between two tangents drawn from an external point P to a circle of radius a and centre O, is 60°, then find the length of OP.
Prove that the tangents drawn at the end points of a chord of a circle make equal angles with the chord.
Long Answer TypeIn the given figure, XY and X’Y’ are two parallel tangents to a circle with centre O and another tangents AB with point of contact C, is intersecting XY at A and X’Y’ at B. Prove that ∠AOB = 90°.
Multiple Choice QuestionsIn Fig., the sides AB, BC and CA of a triangle ABC, touch a circle at P, Q and R respectively. If PA = 4 cm, BP = 3 cm and AC = 11 cm, then the length of BC (in cm) is
11
10
14
15
Switch
