22. In figure, EF is a line passing through the centre O of a circle. If EF bisects chords AB and CD of the circle, prove that AB || CD.

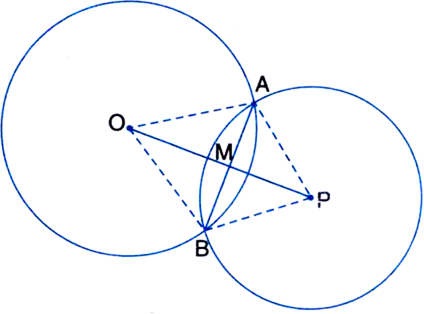
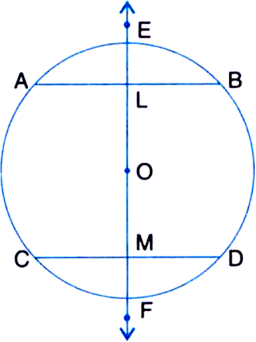
Given: In figure, EF is a line passing through the centre O of a circle. EF bisects chords AB and CD of the circle.
To Prove: AB || CD.
Proof: ∵ EF bisects chord AB
∴ OL bisects chord AB
∴ ∠OLB = ∠OLA = 90°    ...(1)
| ∵    The line drawn through the centre of a circle to bisect a chord is perpendicular to the chord
∵ EF bisects chord CD
∴ OM bisects chord CD
∴ ∠OMC = ∠OMD = 90°    ...(2)
| ∵    The line drawn through the centre of a circle to bisect a chord is perpendicular to the chord
From (1) and (2),
∠OLB = ∠OMC = 90°
But these angles form a pair of equal alternate interior angles
∴ AB || CD.