Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Circles

Short Answer Type

21. If two circles intersect at two points, prove that their centres lie on the perpendicular bisector of the common chord.

495 Views

22. In figure, EF is a line passing through the centre O of a circle. If EF bisects chords AB and CD of the circle, prove that AB || CD.

776 Views

23. Two chords PQ and RS of a circle are parallel to each other and AB is the perpendicular bisector of PQ. Without using any construction, prove that AB bisects RS.

1391 Views

24. OD is perpendicular to chord AB of a circle whose centre is O. If BC is a diameter, prove that CA = 2OD.

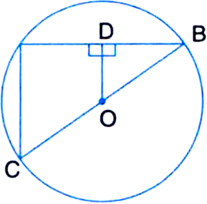
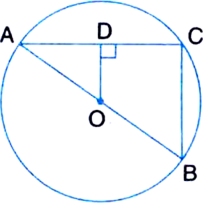
Given: OD is perpendicular to chord AB of a circle where centre is O. BC is a diameter of the circle.
To Prove: CA = 2OD
Proof: ∵ OD ⊥ AB
∴ D is the mid-point of AB
| The perpendicular drawn from the centre of a circle to a chord bisects the chord.
In ∆BAC,
∵ D is the mid-point of AB and O is the midpoint of BC
OD || AC | By mid-point theorem

$and space space space space space space space space OD space equals 1 half space AC rightwards double arrow space space space space space space space space space space CA space equals space 2 space OD$

1805 Views

25. In the figure, diameter AB and a chord AC have a common end point A. If the length of AB is 20 cm and of AC is 12 cm, how far is AC from the centre of the circle?

233 Views

26. Bisector AD of ∠BAC of ∆ABC passes through the centre of the circumcircle of ∆ABC as shown in the figure. Prove that AB = AC.

153 Views

27. How will you complete an arc of a circle?

93 Views

28. Find the length of a chord which is at a distance of 3 cm from the centre of a circle whose radius is 5 cm.

367 Views

29. Two concentric circles are with centre O. A, B, C, D are the points of intersection with a line. If AD = 12 cm and BC = 8 cm, find the length of AB, CD, AC and BD.

167 Views

30. Find the length of a chord of a circle which is at a distance of 4 cm from the centre of the circle with radius 5 cm.

97 Views