26. Bisector AD of ∠BAC of ∆ABC passes through the centre of the circumcircle of ∆ABC as shown in the figure. Prove that AB = AC.

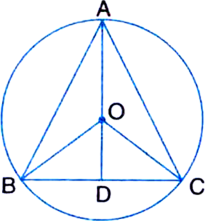
Given: Bisector AD of ∠BAC of ∆ABC passes through the centre of the circumcircle of ∆ABC.
To Prove: AB = AC
Proof: In ∆OAB,
∵ OA = OB | Radii of the same circle
∴ ∠OAB = ∠OBA    ...(1)
| Angles opposite to equal sides of a triangle are equal
Similarly, from ∆OAC,
∠OAC = ∠OCA    ...(2)
But ∠OAB = ∠OAC    ...(3) | Given
∴ ∠OAB = ∠OBA = ∠OAC = ∠OCA ... (4)
| From (1), (2) and (3)
Now, in ∆AOB and ∆AOC,
∠OAB = ∠OAC    | From (4)
∠OBA = ∠OCA    I From (4)
OA = OA    | Common
∴ ∆AOB ≅ ∆AOC
| AAS congruence rule
∴ AB = AC    | C.P.C.T.