Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Circles

Short Answer Type

41.

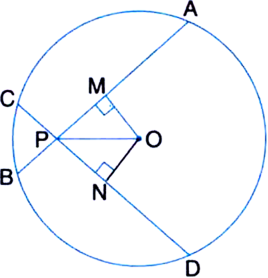
In figure, AB and CD are equal chords of a circle whose centre is O. If OM ⊥ AB and ON ⊥ CD, prove that ∠OMN = ∠ONM.

143 Views

42.
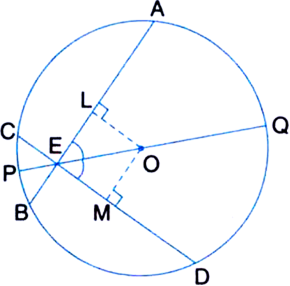
AB and CD are equal chords of a circle whose centre is O. When produced, these chords meet at E. Prove that EB = ED and AE = CE.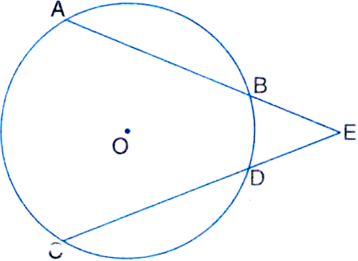

Given: AB and CD are equal chords of a circle whose centre is O. When produced, these chords meet at E.
To Prove: EB = ED and AE = CE.

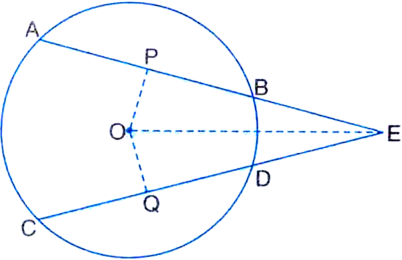
Given: AB and CD are equal chords of a circle whose centre is O. When

Construction: From O draw OP ⊥ AB and OQ ⊥ CD. Join OE.
Proof: ∵ AB = CD    | Given
∴ OP = OQ
| ∵ Equal chords of a circle are equidistant from the centre
Now in right ∆s OPE and OQE,
Hyp. OE = Hyp. OE    | Common
Side OP = Side OQ    | Proved above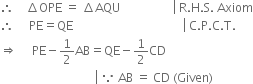

$therefore space space space space increment OPE space equals space increment AQU space space space space space space space space space space space space space space space space space space left enclose space straight R. straight H. straight S. space Axiom end enclose therefore space space space space space PE equals QE space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space left enclose space straight C. straight P. straight C. straight T. end enclose rightwards double arrow space space space space space PE minus 1 half AB equals QE minus 1 half CD space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space left enclose space because space AB space equals space CD space left parenthesis Given right parenthesis end enclose$

$rightwards double arrow$ PE - PB = QE - QD
$rightwards double arrow$ EB = ED Proved.
$rightwards double arrow$ BE + AB = ED + CD    $left enclose space space space because space space AB equals CD end enclose$
$rightwards double arrow$ AE = CE

1293 Views

43. Bisector AD of ∠BAC of ∆ABC passes through the centre O of the circumcircle of ∆ABC. Prove that AB = AC.

198 Views

44. In figure, AB and AC are two equal chords of a circle whose centre is O. If OD ⊥ AB and OE ⊥ AC, prove that ADE is an isosceles triangle.

509 Views

45. If two intersecting chords of a circle make equal angles with the diameter passing through their point of intersection, prove that the chords are equal.

256 Views

46. In figure, AB and CD are two chords of a circle with centre O. The two chords intersect each other at the point P. If PO bisects ∠APD, prove that AB = CD.

129 Views

47. In the given figure, two chords AB and CD of a circle, with centre O, are such that OP and OQ, the perpendiculars from the centre to the chords, are equal. Show that AB = CD.

138 Views

48. Prove that the line segment joining the mid-points of two equal chords of a circle makes equal angles on its same side with the chords.

201 Views

49. Prove that the chords equidistant from the centre of a circle are equal in length.

206 Views

50. PQ and RQ are chords of a circle equidistant from the centre. Prove that the diameter passing through Q is the bisector of ∠PQR.

131 Views

Previous Year Papers

Test Series

Test Yourself

Short Answer Type

42. AB and CD are equal chords of a circle whose centre is O. When produced, these chords meet at E. Prove that EB = ED and AE = CE.

42.
AB and CD are equal chords of a circle whose centre is O. When produced, these chords meet at E. Prove that EB = ED and AE = CE.