 Short Answer Type
Short Answer TypeIn figure A,B and C are three points on a circle with centre O such that ‚ą† BOC = 30¬į and ‚ą† AOB = 60¬į. If D is a point on the circle other than the arc ABC, find ‚ą†ADC.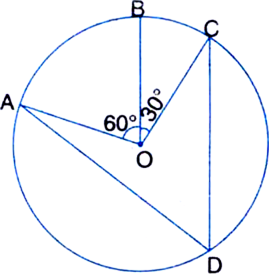
 Long Answer Type
Long Answer Type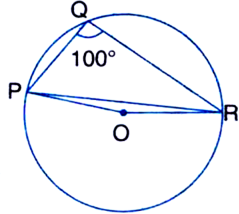
 Short Answer Type
Short Answer Type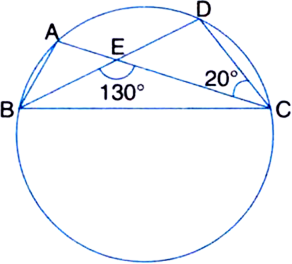
 Long Answer Type
Long Answer TypeIn ‚ąÜOAB and ‚ąÜOCD,
OA = OC | Radii of a circle
OB = OD | Radii of a circle
‚ą†AOB = ‚ą†COD
| Vertically Opposite Angles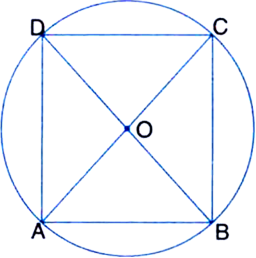
‚ąī ‚ąÜOAB ‚ČÖ ‚ąÜOCD ¬†¬†¬†¬†| SAS Rule
‚ąī AB = CD ¬†¬†¬†¬†| C.P.C.T.
⇒ Arc AB = Arc CD    ...(1)
Similarly, we can show that
Arc AD = Arc CB    ...(2)
Adding (1) and (2), we get
Arc AB + Arc AD = Arc CD + Arc CB
⇒     Arc BAD = Arc BCD
‚áí BD divides the circle into two equal parts (each a semicircle)
‚ąī ‚ą†A = 90¬į, ‚ą†C = 90¬į
| Angle of a semi-circle is 90¬į
Similarly, we can show that
‚ą†B = 90¬į, ‚ą†D = 90¬į
‚ąī ‚ą†A = ‚ą†B = ‚ą†C = ‚ą†D = 90¬į
‚ąī ABCD is a rectangle.
If the non-parallel sides of a trapezium are equal, prove that it is cyclic. Prove that an isosceles trapezium is cyclic.
