 Short Answer Type
Short Answer TypeIn figure A,B and C are three points on a circle with centre O such that ∠ BOC = 30° and ∠ AOB = 60°. If D is a point on the circle other than the arc ABC, find ∠ADC.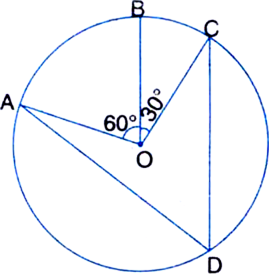
 Long Answer Type
Long Answer Type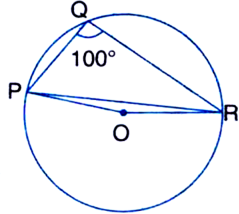
 Short Answer Type
Short Answer Type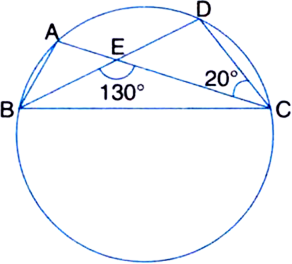
 Long Answer Type
Long Answer TypeIf the non-parallel sides of a trapezium are equal, prove that it is cyclic. Prove that an isosceles trapezium is cyclic.
Given: ABCD is a trapezium whose two non-parallel sides AD and BC are equal.
To Prove: Trapezium ABCD is cyclic.
Construction: Draw BE || AD.
Proof: ∵ AB || DE | Given
AD || BE | By construction
∴ Quadrilateral ABCD is a parallelogram.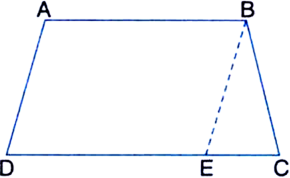
∴ ∠BAD = ∠BED ...(1)
| Opp. ∠s of a || gm
and AD = BE ...(2)
| Opp. sides of a || gm
But AD = BC ...(3) | Given
From (2) and (3),
BE = BC
∴ ∠BEC = ∠BCE ...(4)
| Angles opposite to equal sides
∠BEC + ∠BED = 180°
| Linear Pair Axiom
⇒ ∠BCE + ∠BAD = 180°
| From (4) and (1)
⇒ Trapezium ABCD is cyclic.
| ∵ If a pair of opposite angles of a quadrilateral is 180°, then the quadrilateral is cyclic
