 Short Answer Type
Short Answer Type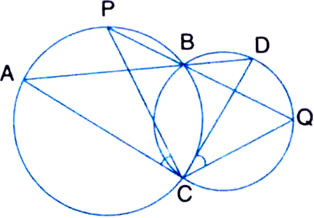
Given: Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively.
To Prove: ∠ACP = ∠QCD.
Proof: ∠ACP = ∠ABP ...(1)
| Angles in the same segment of a circle are equal
∠QCD = ∠QBD ...(2)
| Angles in the same segment of a circle are equal
∠ABP = ∠QBD ...(3)
| Vertically Opposite Angles
From (1), (2) and (3),
∠ACP = ∠QCD.
ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠ CAD = ∠ CBD.
 Long Answer Type
Long Answer Type
 Short Answer Type
Short Answer Type
 Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type