 Short Answer Type
Short Answer Type
Given: Circles are described with sides AB and AC of a triangle ABC as diameters. They intersect at a point D.
To Prove: D lies on the third side BC of ∆ABC.
Construction: Join AD.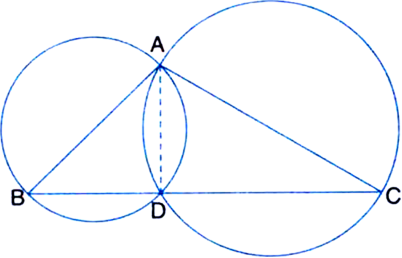
Proof: ∵ Circle described on AB as diameter intersects BC in D.
∴ ∠ADB = 90°
| Angle in a semi-circle
But ∠ADB + ∠ADC = 180°
| Linear Pair Axiom
∴ ∠ADC = 90°.
Hence, the circle described on AC as diameter must pass through D.
Thus, the two circles intersect in D.
Now, ∠ADB + ∠ADC = 180°.
∴ Points B, D, C are collinear.
∴ D lies on BC.
ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠ CAD = ∠ CBD.
 Long Answer Type
Long Answer Type
 Short Answer Type
Short Answer Type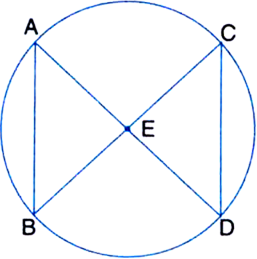
 Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type