 Short Answer Type
Short Answer Type
ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠ CAD = ∠ CBD.
Given: ABC and ADC are two right triangles with common hypotenuse AC.
To Prove: ∠CAD = ∠CBD.
Proof: ∵ AC is the common hypotenuse, ABC and ADC are two right triangles.
∴ ∠ABC = 90° = ∠ADC
⇒ Both the triangles are in the same semicircle.
∴ Points A, B, D and C are concyclic.
∵ DC is a chord
∴ ∠CAD = ∠CBD.
| ∵ Angles in the same segment are equal.
 Long Answer Type
Long Answer Type
 Short Answer Type
Short Answer Type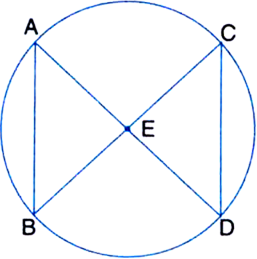
 Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type