 Short Answer Type
Short Answer Type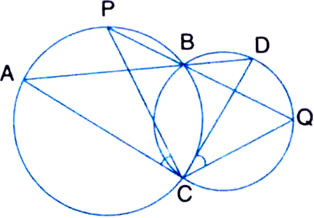
ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠ CAD = ∠ CBD.
Prove that a cyclic parallelogram is a rectangle.
Given: ABCD is a cyclic parallelogram.
To Prove: ABCD is a rectangle.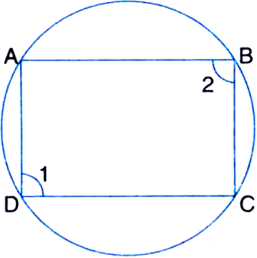
Proof: ∵ ABCD is a cyclic quadrilateral
∴ ∠1 + ∠2 = 180° ...(1)
| ∵ Opposite angles of a cyclic quadrilateral are supplementary
∴ ABCD is a parallelogram
∴ ∠1 = ∠2 ...(2)
| Opp. angles of a || gm
From (1) and (2),
∠1 = ∠2 = 90°
∴ || gm ABCD is a rectangle.
 Long Answer Type
Long Answer Type
 Short Answer Type
Short Answer Type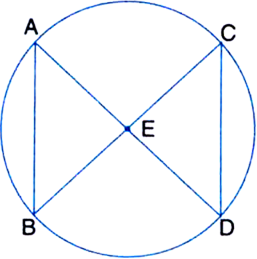
 Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type