Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Circles

Short Answer Type

61. Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see figure). Prove that ∠ACP = ∠QCD.

171 Views

62. If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lies on the third side.

294 Views

63.

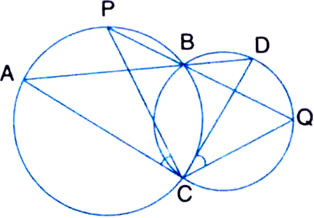
ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠ CAD = ∠ CBD.

398 Views

64.

Prove that a cyclic parallelogram is a rectangle.

1183 Views

Long Answer Type

65. ABCD is a cyclic trapezium with AD || BC. If ∠B = 70°, determine other three angles of the trapezium.

650 Views

66. In figure, a diameter AB of a circle bisects a chord PQ. If AQ || PB, prove that the chord PQ is also a diameter of the circle.

Given: In figure, a diameter AB of a circle bisects a chord PQ. AQ || PB.
To Prove: The chord PQ is also a diameter of the circle.
Proof: ∠AQP = ∠ABP    ...(1)
| Angles in the same segment
∵ AQ || PB and QP intersects them
∴ ∠AQP = ∠QPB    ...(2)
| Alt. Int. ∠s
From (1) and (2),
∠ABP = ∠QPB
⇒    ∠OBP = ∠OPB
∴ OP = OB    ...(3)
| Sides opp. to equal angles
Again,
⇒ ∠BPQ = ∠BAQ    ...(4)
| Angles in the same segment
∵ AQ || PB
and AB intersects them
∴ ∠BPQ = ∠PQA    ...(5)
| Alt. Int. ∠s
From (4) and (5),
∠BAQ = ∠PQA
⇒ ∠OAQ = ∠OQA
∴ OQ = OA    ...(6)
| Sides opp. to equal angles
Adding (3) and (6), we get
OP + OQ = OB + OA
⇒ PQ = AB
∵ AB is a diameter of the circle
∴ PQ is also a diameter of the circle.