 Short Answer Type
Short Answer Type
ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠ CAD = ∠ CBD.
 Long Answer Type
Long Answer Type
 Short Answer Type
Short Answer Type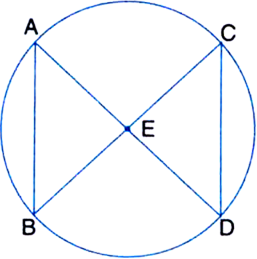
Given: In figure, AB = CD. E is the point of intersection of AD and BC.
To Prove: BE = DE and AE = CE.
Proof: In ∆EAB and ∆ECD,
AB = CD | Given
∠B = ∠D
| Angles in the same segment
∠A = ∠C | Angles in the same segment
∴ ∆EAB ≅ ∆ECD | ASA
∴ BE = DE | C.P.C.T.
and AE = CE. | C.P.C.T.
 Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type