 Short Answer Type
Short Answer Type
ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠ CAD = ∠ CBD.
 Long Answer Type
Long Answer Type
 Short Answer Type
Short Answer Type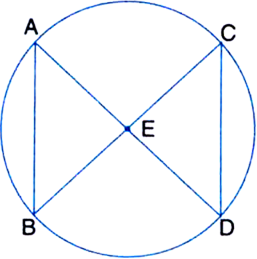
 Long Answer Type
Long Answer TypeGiven: ABCD is a cyclic quadrilateral with AD || BC.
To Prove: AB = DC.
Construction: Join AC.
Proof: ∵ AD || BC
and AC intersects them
∴ ∠ACB = ∠CAD | Alt. Int. ∠s
∴ arc AB ≅ arc CD
| Arcs opposite to equal angles are congruent
∴ chord AB = chord CD
| If two arcs of a circle are congruent, then their corresponding chords are equal
⇒ AB = CD
⇒ AB = DC.
Aliter:
Given: ABCD is a cyclic quadrilateral with AD || BC.
To Prove: AB = DC.
Construction: Draw DE || AB.
Proof: AD || BC | Given
⇒ AD || BE
AB || DE | By const.
∴ Quadrilateral ADEB is a parallelogram
∴ AB = DE ...(1)
| Opp. sides of a || gm are equal
and ∠BAD = ∠BED ...(2)
| Opp. ∠s of a || gm are equal
∵ ABCD is a cyclic quadrilateral
∴ ∠BAD + ∠BCD = 180° ...(3)
| ∵ Opposite angles of a cyclic quadrilateral are supplementary
∠BED + ∠CED = 180° | Linear pair
⇒ ∠BAD + ∠CED = 180° ...(4)
| From (2)
From (3) and (4),
∠BCD = ∠CED
⇒ ∠ECD = ∠CED
∴ DE = DC
| Sides opp. to equal angles
⇒ AB = DC. | From(1)
 Short Answer Type
Short Answer Type