 Short Answer Type
Short Answer Type
ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠ CAD = ∠ CBD.
 Long Answer Type
Long Answer Type
 Short Answer Type
Short Answer Type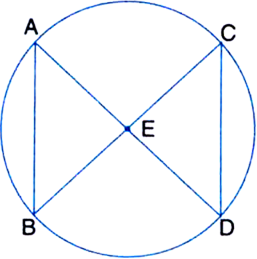
 Long Answer Type
Long Answer Type Short Answer Type
Short Answer TypeGiven: ABCD is a cyclic quadrilateral whose side AB is a diameter of the circle through A,
B, C, D. Also,
∠ADC = 140°.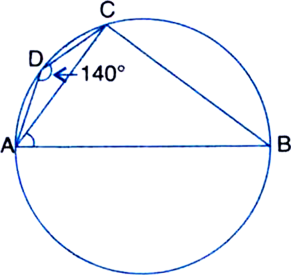
Required: To find ∠BAC.
Determination: ∵ ABCD is a cyclic quadrilateral,
∴ ∠ABC + ∠ADC = 180°
| ∵ Opposite angles of a cyclic quadrilateral are supplementary
⇒ ∠ABC + 140°= 180°
⇒ ∠ABC = 180° - 140° = 40°
Also, ∠ACB = 90°
| ∠ in a semi-circle
Now, in ∆ABC,
∠BAC + ∠ABC + ∠ACB = 180°
| ∵ The sum of the three angles of a ∆ is 180°
⇒ ∠B AC + 40° + 90° = 180°
⇒ ∠BAC + 130° = 180°
⇒ ∠B AC = 180° - 130° = 50°.
