72. Prove that the circle drawn on any equal side of an isosceles triangle as diameter, bisects the third side.  

Given: ABC is an isosceles triangles in which AB = AC. A circle has been drawn with AB as diameter to intersect the third side BC at D.
To Prove: This circle bisects the third side, i.e., BD = DC
Construction: Join AD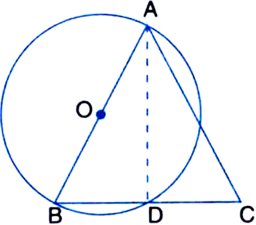

Proof: In ∆ADB and ∆ADC
AB = AC    | Given ...(1)
∠ADB = 90°
| Angle in a semicircle is 90°
∠ADB + ∠ADC =180° | Linear pair
∴ ∠ADB = ∠ADC = 90°    ...(2)
AD = AD    ...(3) | Common
In view of (1), (2) and (3),
∆ADB ≅ ∆ADC
| R.H.S congruence rule
∴ BD = CD    | C.P.C.T.
⇒ D is the mid-point of BC.