76. If the bisectors of the opposite angles of a cyclic quadrilateral ABCD intersect the circle circumscribing it at the points P and Q, prove that PQ is a diameter of the circle.

Given: ABCD is a cyclic quadrilateral. The bisectors of its opposite angles A and C intersect the circle circumscribing it at the points P and Q respectively.
To Prove: PQ is a diameter of the circle.
Construction: Join AQ
Proof: ∵ ABCD is a cyclic quadrilateral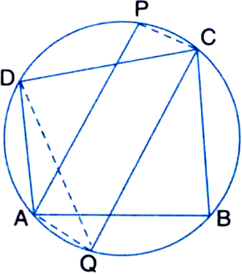

∴ ∠A + ∠C = 180°
| Opposite angles of a cyclic quadrilateral are supplementary

⇒ ∠PAB + ∠BCQ = 90°
But    ∠BCQ = ∠BAQ
| Angles in the same segment of a circle are equal
∴ ∠PAB + ∠BAQ = 90°
⇒    ∠PAQ = 90°
⇒ ∠PAQ is in a semicircle
⇒ PQ is a diameter of the circle