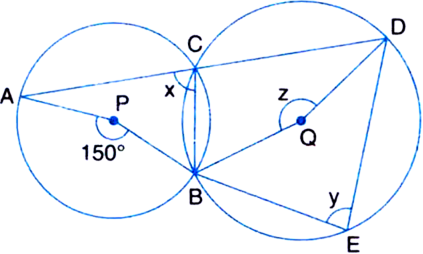
Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type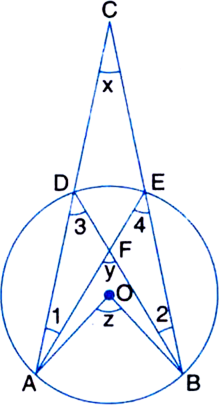
Given: O is the centre of a circle.
To Prove: x + y = z
Proof: ∠3 = ∠4
| Angles in the same segment of a circle are equal
∠z = 2∠3
⇒ ∠z = ∠3 + ∠3
⇒ ∠z = ∠3 + ∠4 ...(1)
∠y = ∠3 + ∠1 ...(2)
| An exterior angle of a triangle is equal to the sum of its two interior opposite angles
(1) - (2) gives
∠z - ∠y = ∠4 - ∠1 ...(3)
∠4 = ∠x + ∠1
| An exterior angle of a triangle is equal to the sum of its two interior opposite angles
⇒ ∠4 - ∠1 = ∠x ...(4)
From (3) and (4),
∠z - ∠y = ∠x
⇒ ∠x + ∠y = ∠z
⇒ x + y = z
5. In the given figure, find the values of a, b, c and d. Given that ∠BCD = 43° and ∠BAE = 62°.