Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

81. In the figure, chord AB of a circle with centre O, is produced to C such that BC = OB. CO is joined and produced to meet the circle in D. If ∠ACD = y and ∠AOD = x, show that x = 3y.

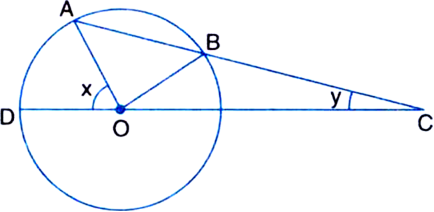
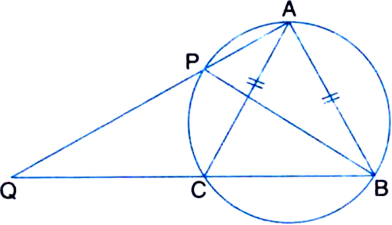
Given: Chord AB of a circle with centre
O, is produced to C such that BC = OB. CO is joined and produced to meet the circle in D. ∠ACD = y and ∠AOD = x.
To Prove: x = 3y
Proof: In ∆BOC
∵ BC = OB
∴ ∠BOC = ∠BCO
| Angles opposite to equal sides of a triangle are equal
⇒    ∠BOC = y    ...(1)
In ∆BOC,
∠OBA = ∠BOC + ∠BCO
| ∵ An exterior angle of a triangle is equal to the sum of its two interior opposite angles
= y + y
= 2y    ...(2)
In ∆OAB,
∵ OA = OB
| Radii of the same circle
⇒ ∠OAB = ∠OBA
| Angles opposite to equal sides of a triangle are equal
⇒    ∠OAB = 2y    ...(3)
Now, ∵ DOC is a straight line
∴ ∠AOD + ∠AOB + ∠BOC = 180°
⇒ x + {180° - (∠OAB + ∠OBA)} + y = 180°
| Angle sum property of a triangle
⇒    x + 180° - (2y + 2y) + y = 180°
⇒    x = 3y

702 Views

82. ABC is a triangle and P is a point on the side BC such that AB = A P. If AP produced meets the circumcircle of ∆ABC at Q, prove that CP = CQ.

259 Views

Short Answer Type

83. The bisector of ∠B of an isosceles triangle ABC with AB = AC meets the circumcircle of ∆ABC at P as shown in the figure. If AP is produced and meets BC produced at Q, prove that CQ = CA.

203 Views

84. D is a point on the circumference of circumcircle of ∆ABC in which AB = AC such that B and D are on opposite sides of AC. If CD is produced to point E such that CE = BD, prove that AD = AE.

268 Views

85. In figure, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠AEB = 60°.

283 Views

86. Two circles intersect at two points A and B. AD and AC are diameters of the two circles (see figure). Prove that B lies on the line segment DC.

184 Views

87. Prove that the quadrilateral formed (if possible) by the internal angle bisectors of any quadrilateral is cyclic.

178 Views

88. ABCD is a cyclic quadrilateral in which AC and BD are its diagonals. If ∠DBC = 55° and ∠BAC = 45°, find ∠BCD.

114 Views

89. Prove that “The angle subtended by an arc at the centre is double the angled subtended by it at any point on the remaining part of the circle.”

112 Views

90. In the figure, O is the centre of the circle. Arc BCD subtends an angle of 140° at the centre. BC is produced to P and CD is joined. Find measure of ∠DCP.