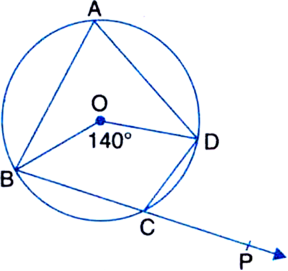
Long Answer Type
Long Answer Type
 Short Answer Type
Short Answer Type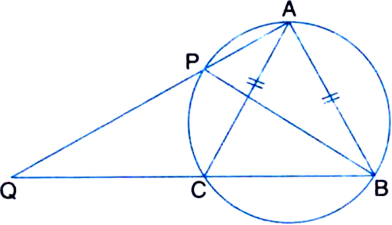
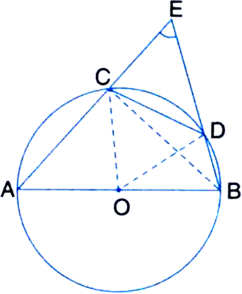
Given: The bisector of ∠B of an isosceles triangle ABC with AB = AC meets the circumcircle of ∆ABC at P. AP is produced and meets BC produced at Q.
To Prove: CQ = CA
Proof: ∠ACB = ∠AQC + ∠QAC ...(1)
| An exterior angle of a triangle is equal to the sum of its two interior opposite angles
∵ AB = AC
∴ ∠ABC = ∠ACB ...(2)
| Angles opposite to equal sides of a triangle are equal
⇒ 2 ∠PBC = ∠AQC + ∠QAC
| ∵ BP bisects ∠ABC and using(1)
But ∠QAC = ∠PBC
| Angles in the same segment of a circle are equal
∴ 2 ∠PBC = ∠AQC + ∠PBC
⇒ ∠PBC = ∠AQC
⇒ ∠PAC = ∠AQC
| ∵ ∠PAC = ∠PBC (Angles in the same segment)
⇒ ∠QAC = ∠AQC
⇒ CQ = CA.
| Sides opposite to equal angles of a triangle are equal