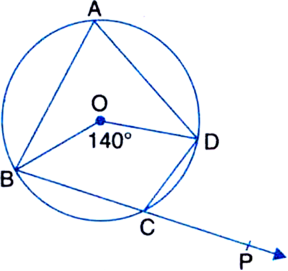
Long Answer Type
Long Answer Type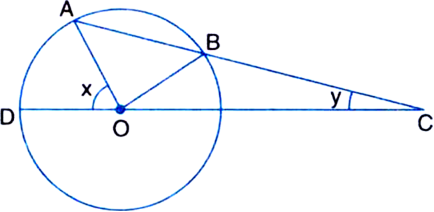
 Short Answer Type
Short Answer Type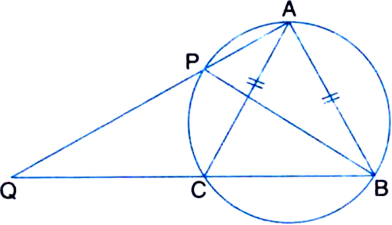
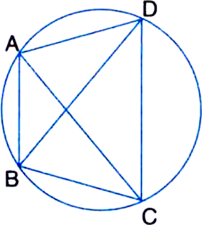
Given: D is a point on the circumference of circumcircle of ∆ABC in which AB = AC such that B and D are on opposite sides of AC. CD is produced to point E such that CE = BD.
To Prove: AD = AE
Proof: In ∆ACE and ∆ABD,
∠ACE = ∠ABD
| Angles in the same segment of a circle are equal
AC = AB | Given
CE = BD | Given
∴ ∆ACE ≅ ∆ABD
| SAS congruence rule
∴ CE = BD | C.P.C.T.