Short Answer TypeIn the figure below, ABC is a triangle in which ∠BAC = 30°. Show that BC is equal to radius of the circumcircle where centre is O.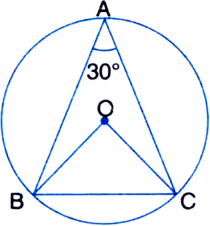
Long Answer TypeTwo chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
The lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance 4 cm from the centre, what is the distance of the other chord from the centre?
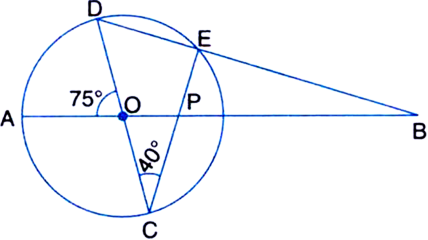
Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
Short Answer TypeLong Answer TypeAC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD are diameters, (ii) ABCD is a rectangle.
Given: AC and BD are chords of a circle that bisect each other.
To Prove: (i) AC and BD are diameters
(ii) ABCD is a rectangle.
Construction: Join AB, BC, CD and DA.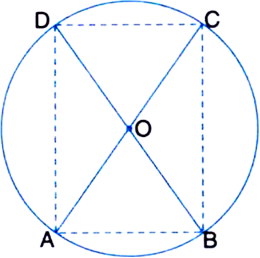
Proof: (i) ∵ ∠A = 90°
∴ BD is a diameter
| ∵ Angle in a semi-circle is 90°
∵ ∠D = 90°
∴ AC is a diameter
| ∵ Angle in a semi-circle is 90°
Thus, AC and BD are diameters.
(ii) Let the chords AC and BD intersect each other at O. Join AB, BC, CD and DA.
In ∆OAB and ∆OCD,
OA = OC | Given
OB = OD | Given
∠AOB = ∠COD | Vert. opp. ∠s
∴ ∆OAB ≅ ∆OCD | SAS
∴ AB = CD | C.P.C.T.
Similarly, we can show that
Adding (1) and (2), we get
⇒ BD divides the circle into two equal parts (each a semi-circle) and the angle of a semi-circle is 90°.
∴ ∠A = 90° and ∠C = 90°
Similarly, we can show that
∠B = 90° and ∠D = 90°
∴ ∠A = ∠B = ∠C = ∠D = 90°
⇒ ABCD is a rectangle.
Switch
