Short Answer TypeGiven: Two congruent circles intersect each other at points A and B. A line through A meets the circles in P and Q.
To Prove: BP = BQ.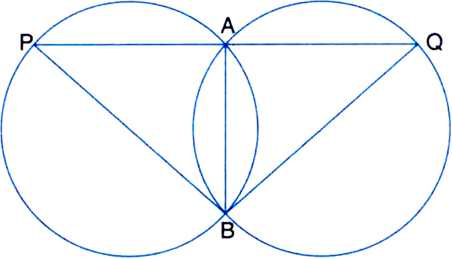
Proof: ∵ AB is the common chord of the two congruent circles
∴ ∠APB = ∠AQB
| ∵ Angles subtended by equal chords are equal
∴ BP = BQ.
| Sides opposite to equal angles are equal
Long Answer TypeIn any triangle ABC, if the angle bisector of ∠A and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the triangle ABC.
Multiple Choice Questionsoutside the circle
inside the circle
Switch
