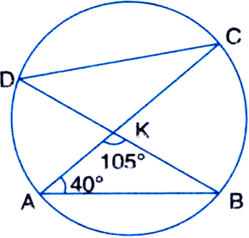
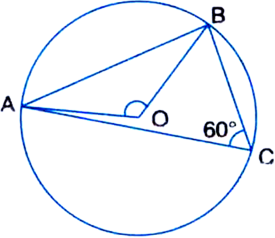
Short Answer Type
Short Answer Type Long Answer Type
Long Answer TypeIn any triangle ABC, if the angle bisector of ∠A and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the triangle ABC.
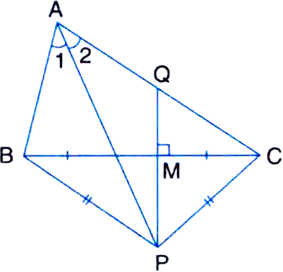
In ∆BMP and ∆CMP.
BM = CM | Given
BP = CP | By (1)
MP = MP | Common
∴ ∆BMP ≅ ∆CMP | SSS
∴ ∠BMP = ∠CMP | C.P.C.T.
But ∠BMP + ∠CMP = 180°
| Linear Pair Axiom
∴ ∠BMP = ∠CMP = 90°
⇒ PM is the right bisector of BC.
Aliter:
Assume that C does not lie on the circle through A, B and P. Let this circle intersect the side AC at C'. (Say)
∠APB = ∠ACB | Given
∠APB = ∠AC'B
| Angles in the same segment
∴ ∠ACB = ∠AC'B
⇒ C and C' coincide
⇒ The assumption that the point C does not lie on the circle is false.
∴ A, B, P and C are concyclic.
 Multiple Choice Questions
Multiple Choice Questionsoutside the circle
inside the circle