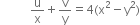40.

If (x + iy)³ = u + iv, then show that  

(x + iy)³ = u + iv

   u +  iv = x³ + i³y³ + 3ixy ( x+ iy)

             = x³ + iy³ + 3ix²y -3xy²

u + iv = (x³ - 3xy² ) + i (3x²y - y³)

Equating real and imaginary parts, we get
                       u = x³ + iy³ + 3ix²y               and         v = 3x²y - y³ 

                   u = x(x² - 3y²)                      and         v = y(3x² - y²)

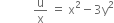                               and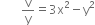    


Adding, we have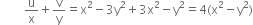   

Hence,