Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Complex Numbers and Quadratic Equations

Short Answer Type

41.

Find the number of non-zero integral solutions of the equation.

$space space space space space space space space space space space space open vertical bar 1 minus straight i close vertical bar to the power of straight x space equals 2 to the power of straight x space end exponent$

150 Views

42.

If $space space straight alpha space and space straight beta$ are two different complex number with $space space space space space space space open vertical bar straight beta close vertical bar space equals space 1 space then space find space open vertical bar fraction numerator straight beta minus straight alpha over denominator 1 minus top enclose straight alpha straight beta end fraction close vertical bar$

149 Views

43.
If (a + ib) (c+id)(e+if)(g+ih) = A+iB, then show that : (a²+ b²) (c²+ d²) (e²+ f²) (g²h²) = A²+ B²

Here, (a + ib) (c+id)(e+if)(g+ih) = A+iB

Taking modulus, on both sides, we get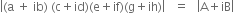

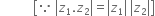
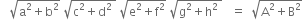
Squaring both sides, we get

(a²+ b²) (c²+ d²) (e²+ f²) (g²h²) = A²+ B²

117 Views

44.

Convert the following in the polar form.

$space space space space space space space space left parenthesis straight i right parenthesis space space space space space fraction numerator 1 plus 7 straight i over denominator left parenthesis 2 minus straight i right parenthesis squared end fraction space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space left parenthesis ii right parenthesis space space space space space fraction numerator 1 plus 2 straight i over denominator 1 minus 3 straight i end fraction$

112 Views

45.

Find the values of x and y, if.

3x + (-2x + y) i = 6-2i

121 Views

46.

Find the values of x and y, if.

(2x + y - 5) + (3x - 2y - 4) i = 0

123 Views

47.

Find the values of x and y, if.

$space space space space space space space space space space fraction numerator open parentheses 1 space plus space straight i close parentheses space straight x space minus space 2 straight i over denominator 3 space plus space straight i end fraction plus fraction numerator left parenthesis 2 minus 3 straight i right parenthesis space straight y space plus space straight i over denominator 3 space minus space straight i end fraction space equals space straight i$

144 Views

48.

Write the conjugates of the following complex numbers :

$space space space space space space space space space space space minus space 5 space plus 1 half straight i$

115 Views

49.

Write the conjugates of the following complex numbers :

$space space space space space space space space space 7 over 5$

123 Views

50.

Write the conjugates of the following complex numbers :

$<pre>uncaught exception: mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56 #0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>$

111 Views

Previous Year Papers

Test Series

Test Yourself

Short Answer Type

43. If (a + ib) (c+id)(e+if)(g+ih) = A+iB, then show that : (a2 + b2) (c2 + d2 ) (e2 + f2 ) (g2 h2 ) = A2 + B2

43.
If (a + ib) (c+id)(e+if)(g+ih) = A+iB, then show that : (a²+ b²) (c²+ d²) (e²+ f²) (g²h²) = A²+ B²