Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Conic Section

Short Answer Type

61. Find the equation of the parabola that satisfying the following condition:
Vertex at (0,0), focus on the positive x-axis and length of latus rectum

16 over 9.

104 Views

62. Find the equation of the parabola that satisfying the following condition:
Vertex at (0, 0) focus on the negative side of y-axis and latus rectum equal to it.

91 Views

63. Find the equation of a parabola that satisfies the given condition:
Focus (6, 0), directrix is x = – 6

The focus is S(6, 0) which lies on x-axis.
The directrix is x + 6 = 0 which is a line parallel to y-axis i.e., perpendicular to x-axis.
∴ The parabola is of the standard form $straight y squared equals 4 ax.$
Also, focus (a, 0) $left right arrow$ (6, 0) directrix x + a = 0 is x + 6 = 0 $rightwards double arrow$ a = 6
Hence, the equation of the parabola is $straight y squared equals 4 space left parenthesis 6 right parenthesis space straight x space or space straight y squared equals 24 straight x$

Alternative method:
Let line l be the directrix with equation x + 6 = 0
The focus is S (6, 0). Take a point $straight P space left parenthesis straight alpha comma space straight beta right parenthesis$ on the parabola.
From P, draw PM perpendicular on directrix l and join PS. By definition of parabola, PS = PM
$rightwards double arrow$ d = p
$rightwards double arrow$ $square root of left parenthesis straight alpha minus 6 right parenthesis squared plus left parenthesis straight beta minus 0 right parenthesis squared end root space equals space open vertical bar fraction numerator straight alpha plus 6 over denominator square root of left parenthesis 1 right parenthesis squared plus 0 squared end root end fraction close vertical bar$

$equals square root of left parenthesis straight alpha minus 6 right parenthesis squared plus straight beta squared end root space equals space open vertical bar straight a plus 6 close vertical bar$
Squaring both sides, we get
$space space space space space space straight alpha squared minus 12 straight alpha plus 36 plus straight beta squared space equals space straight alpha squared plus 12 straight alpha plus 36 space rightwards double arrow space straight beta squared minus 24 straight alpha space equals space 0$
Hence, the locus of P i.e., the equation of parabola is $<pre>uncaught exception: mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56 #0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>$

94 Views

64. Find the equation of a parabola that satisfies the given condition:
Focus (0 – 3); directrix y = 3

148 Views

65. Find the co-ordinates of a point on the parabola y² = l8x, where the ordinate is 3 times the abscissa.

165 Views

66. Find the area of the triangle formed by the lines joining the vertex of the parabola x² = 12y to the ends of the latus rectum.

181 Views

67.

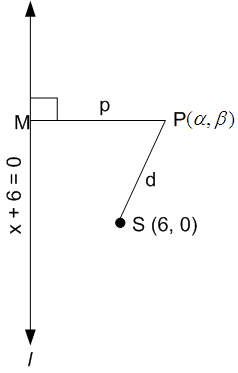
An equilateral triangle is inscribed in the parabola $straight y squared equals 4 ax.$ , where one vertex is at the vertex of the parabola. Find (a) the length of the side of the triangle, (b) area of triangle ABC.

187 Views

68. If a parabolic reflector is 20 cm in diameter and 5 cm deep, find the focus.

91 Views

69. LL' is the latus rectum of a parabola, y² = 4ax, a > 0. Find the co-ordinates of points L and L'.

94 Views

70. LL' is the latus rectum of a parabola, x² = -8y. Find the co-ordinates of points L and L'.

93 Views

Previous Year Papers

Test Series

Test Yourself

Short Answer Type

63. Find the equation of a parabola that satisfies the given condition:Focus (6, 0), directrix is x = – 6

63. Find the equation of a parabola that satisfies the given condition:
Focus (6, 0), directrix is x = – 6